Given a coarse grid, the ideal prolongation operator is defined by 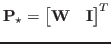, where the weight matrix,  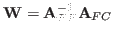, interpolates a set of fine grid variable (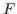-points) from a set of coarse grid variable (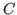-points), and the identity matrix, 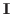, represents the injection of 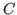-points to and from the coarse grid (Falgout and Vassilevski, 2004). In this talk, we consider 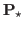, constructed from both traditional  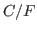splittings and  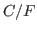splittings corresponding to aggregates, for several challenging problems. We demonstrate the effects of the  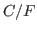splitting on the convergence and complexity of 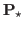. Finally, we argue that  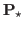may be misleading in demonstrating the ``ideal'' nature of interpolation of a given  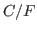splitting by providing numerical evidence that hierarchies built using  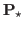converge more slowly than hierarchies built from alternative prolongation operators with the same  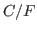splitting. This is important as we wish to minimize the number of levels in a multigrid hierarchy by using a small set of C points for which  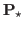may have poor convergence.

Researchers should cite this work as follows:

• Erin Molloy (2016), "Is the Ideal Approximation Operator Always "Ideal" for a Particular C/F Splitting?," https://nanohub.org/resources/23512.

  BibTex | EndNote

1. approximation
2. c/f
3. ideal
4. Illinois
5. NanoBio Node at Illinois
6. operator
7. particular
8. splitting