Nanophotonics
Apps (Ready-to-Use, Interactive, Self-Contained)
Photonics DB: Optical Constants
PhotonicsDB: Optical Constants uses initial experimental data to interpolate the dielectric function or the index of refraction of bulk materials. Interpolations are possible only within a certain range of wavelengths taken from the initial experimental data sets.
The tool also gives the approximate data and the approximation coefficients obtained from best-fit Drude-Lorentz models for gold and silver. Depending on the number of Lorentz kernels (from 1 to 5) the Drude-Lorentz models support different accuracy of the best-fit approximation. In addition to the cubic spline interpolation of the raw experimental data, gold and silver can be interpolated using the corresponding Drude-Lorentz best-fit models.

Nanosphere Optics Lab
Nanosphere Optics Lab uses Mie theory to calculate the absorption, scattering, and extinction spectra of spherical nanoparticles. Calculations for spheres of a constant dielectric, as well as the wavelength dependent dielectric materials gold and silver are possible for a range of particle sizes.
Understanding how light interacts with small particles is necessary for a description of a wide range of physical phenomenon. When electromagnetic radiation is incident on a particle the charges in the material are set in motion. This coupling of the incident field to the charged particles gives rise to absorption, via energy tranfer to the surrounding medium, and scattering, via reradiation of the electromagnetic field.
For objects whose dimensions are much larger than the wavelength of light geometric optics will suffice. However, when the particle size is on the order of the wavelength of light a more complicated approach is necessary. For a solution to this problem we turn to electromagnetic theory in the form of the classical Maxwell's equations. In general, the exact solution of the Maxwell equations for an arbitrary particle is complex. However, we can gain insight into the light-particle interaction by examining the absorption and scattering due to small spherical particles. The formal solution to this problem was first given by Gustav Mie in 1908 and is now known as Mie theory.
The Nanosphere Optics Tool uses Mie theory calculate the absorption, scattering, and extinction, which is the sum of absorption and scattering, for a spherical particle of given radius and dielectric constant. The results of the current simulations are given as extinction factors relative to the expected result from geometric optics.
- Nanosphere Optics Lab is powered by B. T. Draine's modified version of the Mie theory code found in C. F. Bohren, D. R. Huffman "Absorption and Scattering of Light by Small Particles" John Wiley and Sons, Inc., 1983.
- Modified f77 version of Bohren and Huffman's code can be found at B. T. Drain's page:
http://www.astro.princeton.edu/~draine/scattering.html

Nanosphere Optics Lab Field Simulator
This tools allows the study of the interaction of light and matter (nanoparticles). It simulates the electric field induced by electromagnetic radiation on spherical nanoparticles as well as the absorption spectrum.

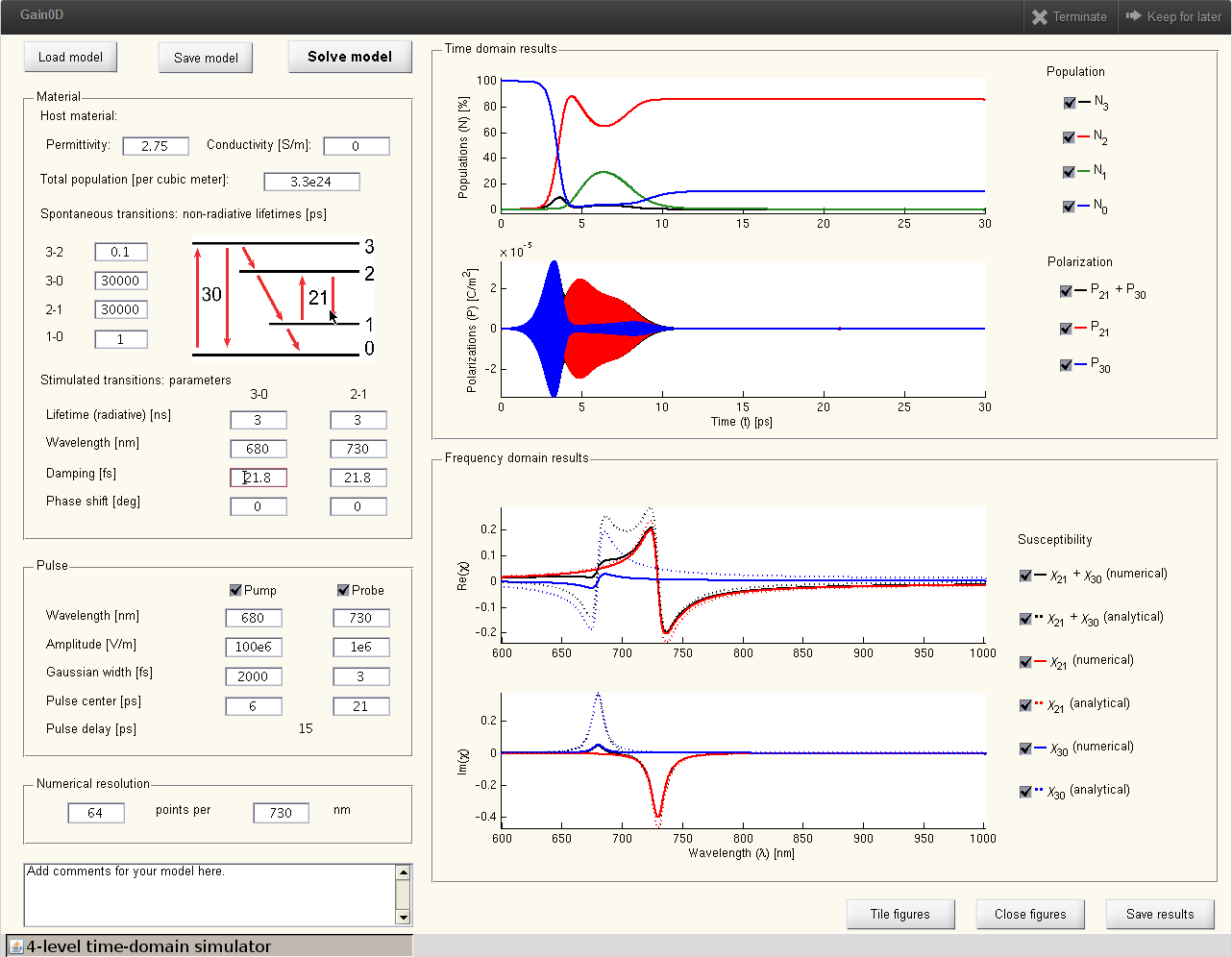
PhotonicsGAIN-0D
A four-level system is a typical model describing the process of lasing. It is widely used to model gain media. PhotonicsGAIN-0D simulates the local response (0-dimenstion) of a generic 4-level system interacting with one or two sequential incident light pulses. The code uses the local electric field, to compute the population kinetics at each energy level, and monitors the polarization evolution in time domain. Then, the effective susceptibility is calculated in frequency domain through the Fast Fourier transform (FFT).
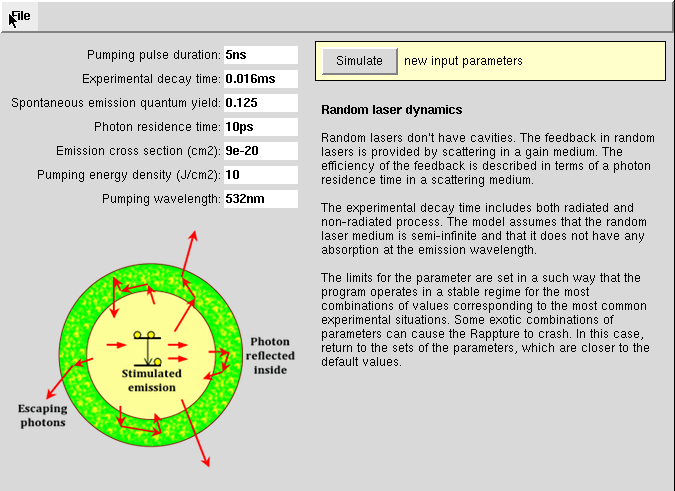
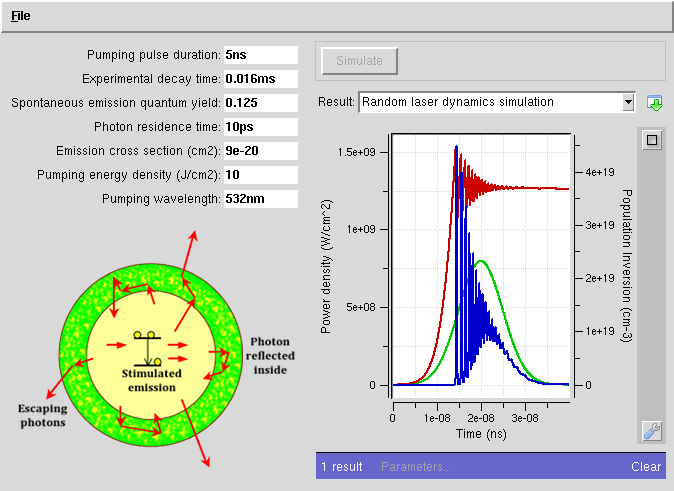
Random Laser Dynamics
Random lasers don’t have cavities. The feedback in random lasers is provided by scattering in a gain medium. The efficiency of the feedback is described in terms of a photon residence time in a scattering medium. The dynamics of the random laser emission is determined by the pumping energy density, the shape and the duration of the pumping pulse (in this model, we assume a gaussian pulse-shape), the emission cross section of the gain medium, and the experimental decay time. The effective absorption length at the pumping pulse duration is determined by the combination of absorption and scattering processes.
The experimental decay time includes both radiated and non-radiated process. The model assumes that the random laser medium is semi-infinite and that it does not have any absorption at the emission wavelength.
This program demonstrates how the stimulated emission dynamics, which often can produce several short stimulated emission pulses in response to a longer pumping pulse, depends on the parameters above. The principles of operation of random lasers can be found in online presentation by Mikhail A. Noginov (Random Lasers – http://nanohub.org/resources/1311) or in the book “ISBN: 978-0-387-23913-2 – M. A. Noginov, Solid-State Random Lasers, Springer, 2005”.
The limits for the parameter are set in a such way that the program operates in a stable regime for the most combinations of values corresponding to the most common experimental situations. Some exotic combinations of parameters can cause the Rappture to crush. In this case, return to the sets of the parameters, which are closer to the default values.
Simple Photonic Crystals
Simple 2D photonic crystals are composed of periodic dielectric structures in a two-dimensional world. Electromagnetic waves in 2D are decomposed into two categories: TE and TM. Maxwell's equations are thus eigenvalue equations solving for TE and TM modes. A set of eigenfrequencies exist for each wavevector k. The plot of frequencies v.s. wavevectors is so-called band diagram.
We explore a set of rods arranged either in square or triangular lattice. The left part of the picture shows solid rods of square lattice in air background, while the right shows air rods of triangular lattice in solid background. The lattice constants are used as length units. We solve the band diagrams for both TE and TM modes. Try it out solving band diagrams for yourselves.


Optical Properties of Single Coaxial Nanowires
This program computes the following optical properties of a single nanowire with up to 2 shell layers using Mie-formalism:
1) Total scattering, absorption and extinction efficiency
2) Absorption efficiency of individual layers
3) The integrated photon flux absorbed and the ideal photocurrent density under AM 1.5 G illumination as a function of layer thickness
4) Electric and magnetic polarizability under TE polarization (E field perpendicular to nanowire axis)

Thermophotonic Selective Emitter Simulation
Thermophotovoltaic (TPV) devices convert heat to electricity using thermal radiation to illuminate a photovoltaic (PV) diode. Typically, this radiation is generated by a blackbody-like emitter. Such an emission spectrum includes a broad range of wavelengths, but only higher energy photons can be converted by the PV diode, which severely limits efficiencies. Thus, introducing a selective emitter and filter to recycle unwanted photons could potentially greatly enhance performance. In this work, we consider a rare earth-doped selective emitter structure to increase the number of photons emitted above the bandgap of the photovoltaic (PV) cell, while minimizing the total power emitted below the bandgap. A chirped dielectric stack, as shown in the figure is introduced on top to limit emitted wavelengths, while a broadband dielectric mirror on the bottom ensures unidirectional emission. We developed a GUI-based tool to precisely calculate the emittance spectrum and efficiency for this design as various parameters, such as the number of dielectric bilayers and PV cell bandgap. Through simulations of chirped dielectric stack structures and coatings on a rare-earth ceramic substrate, it is found that an efficiency of 33.89% is achievable, for a filter bandgap of 0.37 eV and PV bandgap of 0.75 eV. The research thus demonstrates the potential for unprecedented efficiencies of TPV cells. These predictions will be used to experimentally fabricate and characterize these structures.


Active Media FDTD Nanophotonic Device Simulator
The “Active Media FDTD Nanophotonic Device Simulator” is a general computational model of complex material media for electrodynamics simulation using the Finite-Difference Time-Domain (FDTD) method. It is based on a multi-level multi-electron quantum system with electron dynamics governed by Pauli Exclusion Principle, state filling, and dynamical Fermi-Dirac Thermalization, enabling it to treat various solid-state, molecular, or atomic media. The formulation is valid at near or far off resonance as well as at high intensity. We show its FDTD application to a semiconductor in which the carriers’ intraband and interband dynamics, energy band filling, and thermal processes were all incorporated for the first time. The FDTD model is sufficiently complex and yet computationally efficient, enabling it to simulate nanophotonic devices with complex electromagnetic structures requiring simultaneous solution of the mediumfield dynamics in space and time. Applications to direct-gap semiconductors, ultrafast optical phenomena, and multimode microdisk lasers are illustrated.
Illinois Tools: Optics Lab
This tool allows a user to simulate the passage of electromagnetic light through multiple lenses.
Illinois Tools: Bio Photonics Simulator
This tool simulates the passage of light through biological tissue. The injected pulse of light obtained at the screen is analyzed to observe spectral redistribution induced due the spatial co-relation of the tissue sample.
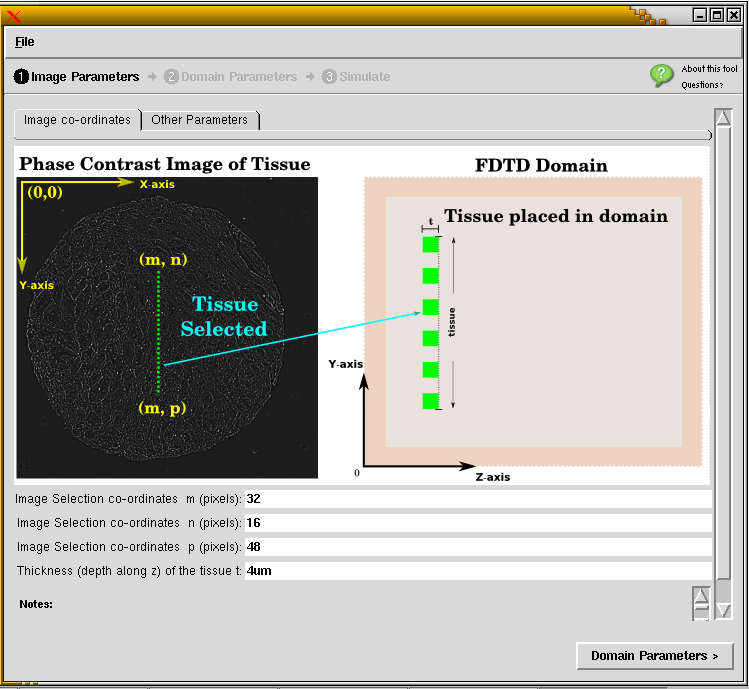

Nano-Bio-Photonics Simulator
This tool simulates the passage of light through biological tissue embedded with metallic nano-particles. The injected pulse of light obtained at the screen is analyzed to observe spectral redistribution induced due the spatial co-relation of the tissue sample.




