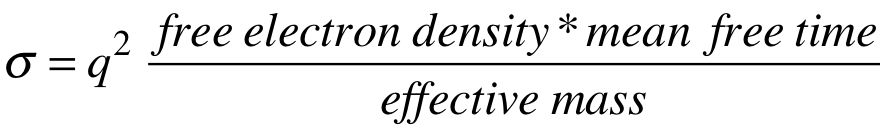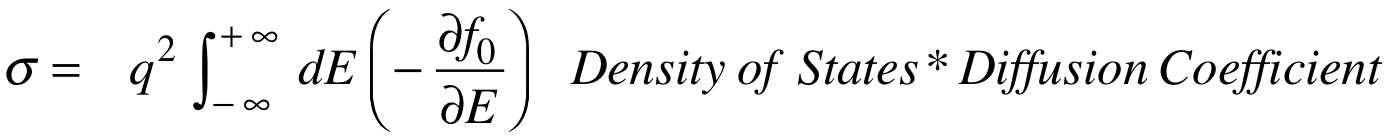How can an elastic resistor dissipate energy? (Updated 9/20/13)

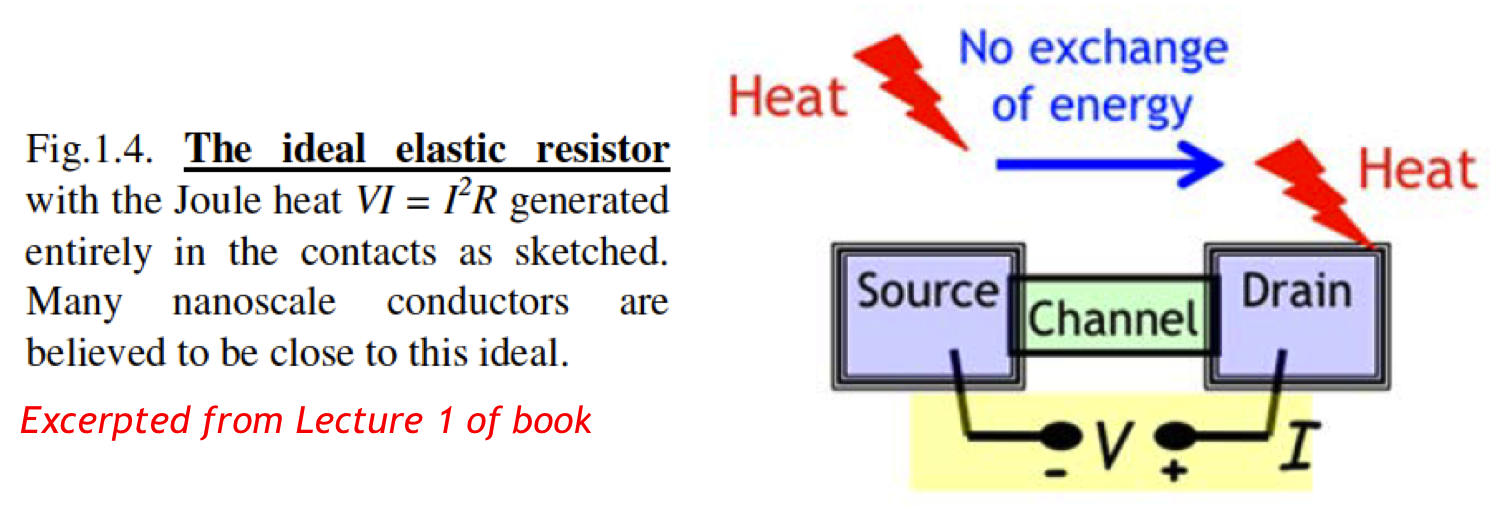
There is experimental evidence that the heat I²R associated with a nanoscale conductor of resistance R is dissipated primarily in the contacts and not in the conductor. See below.

The Landauer model, widely used in mesoscopic physics, assumes the the heat is dissipated entirely in the contacts. My colleague Ashraf often compares the electron to a bullet which dissipates most of its energy in the object that stops it, rather than in the medium it flies through.

This assumption allows a relatively simple description of transport because the entropy-driven processes (heat generation in the contacts) are spatially separated from the potential-driven ones in the channel. Ordinarily the two are intertwined.

Why do you call it a new perspective? Isn’t mesoscopic physics 25+ years old?? (Updated 9/20/13)

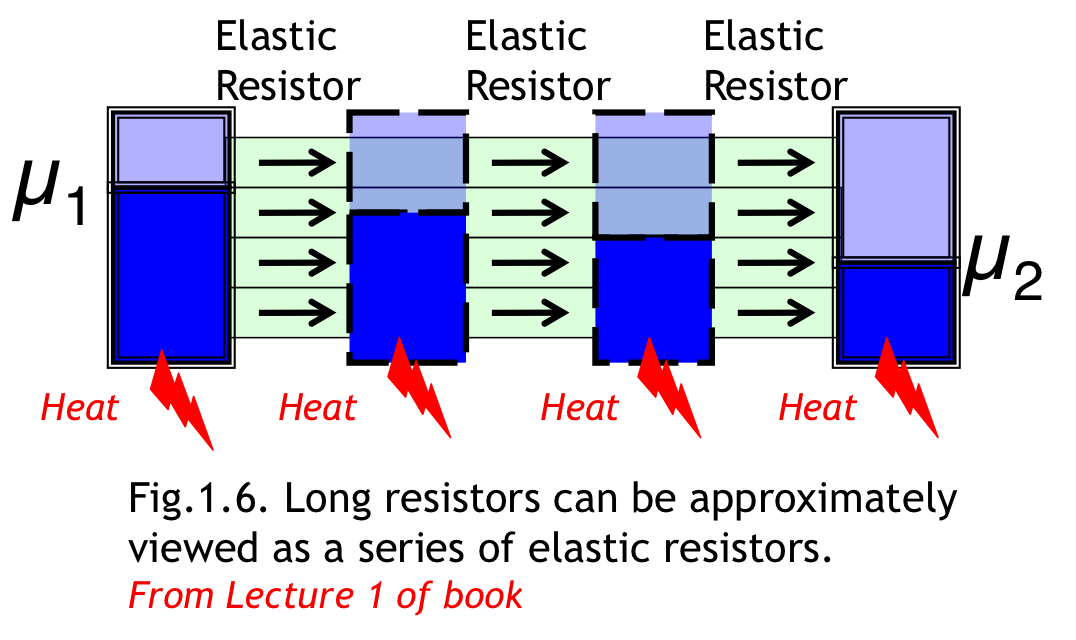
Mesoscopic physics has shown us the utility of the Landauer model for short conductors, but it is generally assumed to be irrelevant for standard transport theory (long conductors) which requires a completely different approach.

We argue in this book that we could use the Landauer model to get insights into long conductors as well by viewing them approximately as a series of elastic resistors, with energy dissipated between sections as shown below.

When used carefully, this viewpoint allows us to obtain many well-known results of transport theory in a relatively straightforward way. We use it to present a consistent view of a wide range of topics involving both semiclassical and quantum transport in both short and long conductors.

This includes (1) conductivity, (2) nanotransistors, (3) nanoscale p-n junctions, (4) thermoelectric coefficients, (5) phonon transport, (6) fuel value of information, (7) resonant tunneling and Anderson localization, (8) quantized conductance, (9) integer quantum Hall effect and (10) spin transport.

Can you give an example? (Updated 9/20/13)

Consider the first item in the list, namely conductivity, a concept that is much older than mesoscopic physics. There are two “textbook” expressions for conductivity: First is the simple Drude formula that appears in “Chapter 1” of all texts

while the second is less familiar:

This expression is much more generally valid but it usually appears much later in any text, because it requires advanced concepts like the Boltzmann or Kubo formalisms.

Note that the second expression involves the derivative of the Fermi function rather than the Fermi function f₀(E). This is usually difficult to understand with elementary arguments, but it comes out of the advanced formalisms. The difference is not significant for non-degenerate conductors, but can be very significant in general.

The Landauer-based approach described above allows us to obtain the second expression using relatively elementary arguments (Lecture 5 of the book).

So this book goes beyond the simple Landauer model used in mesoscopic physics? (Updated 9/20/13)

Yes, we revisit a number of topics like conductivity and thermoelectric coefficients that are much older than mesoscopic physics.

We could call it the LBN (Landauer-Boltzmann-NEGF) approach based on the following observations:

(1) The * Landauer model is a useful idealization that provides a simple intuitive understanding of many well-known results for all conductors, short and long.

(2) These results can all be formally obtained from the * Boltzmann Equation in the semiclassical regime, and from the * NEGF (Non equilibrium Green’s Function) method in general including quantum transport.

Both the Boltzmann and the NEGF methods can incorporate sophisticated microscopic models for scattering and dissipation as needed. The simple Landauer model can be benchmarked against NEGF in general, or against Boltzmann in the semiclassical regime.

All three (L, B and N) can be used both close to equilibrium and far from equilibrium.

Why doesn’t the book use the Kubo formalism? (Updated 9/20/13)

The Kubo formalism is a linear response theory based on small perturbations close to equilibrium.

Many of the problems in modern nanoelectronics require a framework that can handle transport far from equilibrium. All three components of our LBN (Landauer-Boltzmann-NEGF) approach meet this requirement, as noted in question 1.1.3 above.

Does this model agree with the Kubo formalism in the linear response regime close to equilibrium? (Updated 9/20/13)

Yes, an elementary discussion is presented in Lecture 15 of the book.

A number of respected authors have obtained the Landauer formula starting from the Kubo formalism, and this is often regarded as a rigorous proof.

We use NEGF as the rigorous standard, in the spirit of our LBN (Landauer-Boltzmann-NEGF) approach. As noted earlier, there is no intent to slight anyone or any other approach.

Isn’t it a problem to have separate electrochemical potentials in a single system? (Updated 9/20/13)

On the contrary, I would argue that current flow requires separate electrochemical potentials, just as the flow of heat requires separate temperatures.

The Kubo formalism allows us to get around this by relating the linear conductance to the equilibrium noise through the fluctuation-dissipation (F-D) theorem, but this only works for transport close to equilibrium and is not possible in general.

There is nothing fundamentally wrong with invoking two large reservoirs held at two different electrochemical potentials and/or temperatures connected by a nanoscale conductor.

Isn’t it true that sometimes you do have “equilibrium currents” even with a single electrochemical potential?

Yes, but these are distinct from the transport currents we are normally interested in, as evident in the context of edge currents in the quantum Hall regime.

But the Kubo formula uses a single electrochemical potential? (Updated 9/20/13)

Yes, as explained above, the Kubo formula calculates an equilibrium quantity and relates it to the linear transport coefficients through the F-D theorem.

NEGF on the other hand addresses the non-equilibrium problem directly.

Like the Boltzmann equation, NEGF too permits the use of separate electrochemical potentials as boundary conditions.

Isn’t transport essentially a many-body process? (Updated 9/20/13)

Virtually all the textbook results we use to interpret experiments are based on one-electron pictures. In spite of that it is commonly believed that current flow, at least in metals, is a many-body interacting process: One electron does not flow from left to right, it simply pushes the next electron, which pushes the next electron and so on.

But many mesoscopic experiments make me think that the one-electron theory is more than a matter of convenience. For example, in 1985 Richard Webb and collaborators from IBM reported the Aharonov-Bohm (AB) effect in metallic rings with a period described quite well by the one-electron theory, as if we were talking about AB paths in vacuum!

The one-electron picture works so well possibly because there is a Landau-style ( I mean Landau, not Landauer! ) dressed quasi-particle that “actually” moves from left to right. I have some mental pictures of what such a quasi-electron looks like, but I do not know how such pictures could be tested experimentally and I am not aware of any serious discussions along these lines.

Are you saying that there is no evidence of many-body effects in transport experiments? (Updated 9/20/13)

Of course not, special materials and structures are known to exhibit many-body effects under special experimental conditions.

I am just trying to clarify the notion that transport is “essentially” a many-body process.