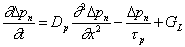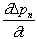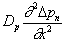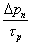Objective of Lesson: To learn how to solve problems for situations in semiconductors using the minority carrier diffusion equations.
Reading Assignment: Sections 3.4.3 and 3.4.4
Homework: Problems 3.16-3.22 in the textbook
What do you need to know for the exam?
1. You must be able to recognize low-level injection conditions under a variety of situations.
Summary
Low-level injection is a really, really important concept in semiconductors because we typically have to assume low-level injection in order to solve problems on paper. This supplement to Lesson 4.4: Simplifying the Minority Carrier Diffusion Equations goes into detail on how to determine whether a semiconductor we are discussing is in low-level injection.
Simplifying the Minority Carrier Diffusion Equations
This lesson is a big deal. It presents the process for solving problems given a situation in a semiconductor. We call this “modeling” semiconductors because through this process gives us greater insight into the microscopic cause of the macroscopic observations we can make. Problems like the example herein will appear on quizzes, an exam, and on the final. It is critical that you understand these techniques if you want to work with semiconductors.
Let’s kick it off with an example.
A uniformly doped, infinite silicon wafer with ND = 1015 cm-3 and NA = 0 cm-3 has been in the dark for a long time. Suddenly light is turned on such that the wafer is
illuminated with a uniform generation rate, Go. Find an equation to describe the behavior of the minority carrier concentration.
The minority carrier diffusion equations (MCDEs) allow us to solve this problem. What this lesson does is lay out the procedure, step-by-step, for solving these kinds of problems. They will always be word problems—descriptions of a situation in a semiconductor we wish to understand better.
The general steps to the solution are:
1. Identify the minority carrier
2. Simplify the appropriate MCDE
3. Find the general solution
4. Identify boundaries and boundary conditions or initial condition
5. Find exact solution
6. Check answer
Step 1. Identify the minority carrier
The problem statement gives the donor and acceptor concentrations (and if one is not given, assume it is zero) so the majority and minority carriers are easily identified using skills developed previously. For this example the minority carriers are the holes. Write down the appropriate MCDE.
Step 2. Simplify the appropriate MCDE
Let’s go term by term. The first term is a partial derivative with respect to time. If the situation described is such that nothing is changing with time, then that term will go to zero. For that to be true, you will see phrases in the problem statement such as “steady-state” or “has been on for a long time.” Sometimes those phrases, however, are simply setting the stage for a change that will occur—mentioned later in the problem statement—and our problem is a good example for this.
The problem statement has the phrase, “has been in the dark for a long time,” but this is immediately followed by, “suddenly light is turned on.” The second phrase suggests a change in time. The problem statement also mentions an “infinite” silicon wafer. This is “code” for saying there are no boundaries or that the boundaries are so far away that they do not influence the region of interest.
Having no boundaries suggests that the 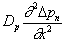 term will go away (be set to zero) because there will be no gradient in the carrier concentration. Keep in mind that at least one of the partial derivative terms must always be eliminated. If both are kept, one must solve the problem using separation of variables, and the result contains an infinite series, not a closed-form solution we can easily recognize and write down.
term will go away (be set to zero) because there will be no gradient in the carrier concentration. Keep in mind that at least one of the partial derivative terms must always be eliminated. If both are kept, one must solve the problem using separation of variables, and the result contains an infinite series, not a closed-form solution we can easily recognize and write down.
Returning to our example, the situation is for an infinite semiconductor where there has been a recent change to the situation—this suggests that we are dealing with a time-domain problem so the first term, 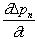 , is retained.
, is retained.
The second term, 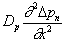 , is harder to explain to a novice. Keep in mind that usually exactly one of the derivative terms is kept. We have reason to keep the time derivative term. We have an infinite semiconductor. We have no indication that there are two locations inside the semiconductor that have different concentrations—you would see boundaries and boundary conditions that have different concentration values if there were. We therefore conclude that the
, is harder to explain to a novice. Keep in mind that usually exactly one of the derivative terms is kept. We have reason to keep the time derivative term. We have an infinite semiconductor. We have no indication that there are two locations inside the semiconductor that have different concentrations—you would see boundaries and boundary conditions that have different concentration values if there were. We therefore conclude that the 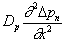 term must be set to zero. That is the best explanation I can give for now.
term must be set to zero. That is the best explanation I can give for now.
The third term, 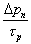 , is the recombination term. It will very rarely be eliminated. The most well-known situation in which it is set to zero is for the very short base of a bipolar junction transistor. In that situation it is set to zero because most of the carriers will cross the region in a time that is very short compared to a lifetime of a carrier. If you are ever in doubt, do not eliminate that term. If you are sure it should be eliminated and it is not for a “very short” region of semiconductor, reconsider. A good physics-based reason to not eliminate the term is that if the semiconductor is out of equilibrium, then the carrier concentrations have usually either been increased or decreased so Δp ≠ 0 so that term is not zero. Think about it. If Δp = 0 everywhere, we have equilibrium or an equilibrium-like situation and that is not very interesting when studying minority carriers. For this example the
, is the recombination term. It will very rarely be eliminated. The most well-known situation in which it is set to zero is for the very short base of a bipolar junction transistor. In that situation it is set to zero because most of the carriers will cross the region in a time that is very short compared to a lifetime of a carrier. If you are ever in doubt, do not eliminate that term. If you are sure it should be eliminated and it is not for a “very short” region of semiconductor, reconsider. A good physics-based reason to not eliminate the term is that if the semiconductor is out of equilibrium, then the carrier concentrations have usually either been increased or decreased so Δp ≠ 0 so that term is not zero. Think about it. If Δp = 0 everywhere, we have equilibrium or an equilibrium-like situation and that is not very interesting when studying minority carriers. For this example the 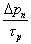 term is retained.
term is retained.
The last term is generation in the semiconductor due to light, GL. The problem statement says that light has been recently turned on—so the light is on. Be careful about using this as a rule. Just because light has been on does not mean it stayed on. A similar problem could state that the light had been on for a long time and then it was turned off. In that case, GL = 0 so the term is eliminated. For this example the light is on and GL = Go.
For this example the GL term is retained.
The table below lists the terms and the typical phrases you need to look for in order to decide whether to eliminate the term. A similar table is in the text.
After the elimination of terms, the MCDE is simplified to, 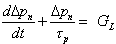 .
.
Note that the partial derivative signs have been exchanged for simple derivatives because one of the derivative terms was eliminated. Now that the MCDE is simplified, the next step is to identify the general solution.
Step 3. Find the general solution
Do you remember your differential equations class? Do you remember terminology such as first order, second order, homogenous equations, or non-homogeneous equation? The equation the MCDE was simplified to is a first-order, non-homogenous equation. It is first-order because it is a first derivative. It is non-homogenous because once all the Δp terms are moved to one side of the equation, the equation is not equal to zero. If you recall from your differential equations course, you always had to solve the homogenous equation first.
One other thing from your differential equations course. The standard technique for solving problems was to see a differential equation…and recall/guess the general solution. The interesting part was identifying and dealing with boundary conditions as they lead to the exact solution. The same approach will be taken in this course and because the emphasis is on finding and working with the exact solution, you will always be provided with the general solutions.
The general solution to the simplified MCDE above is, 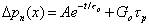 .
.
The table below lists the differential equations you will encounter when working with semiconductors and the corresponding general solutions.
Step 4. Identify boundaries and boundary conditions or initial condition
For the time domain we call the boundary condition the initial condition. There is some indication of a change in a time-domain problem, and that point is usually called the initial time or t = 0. For this problem it is when the light is turned on. So what is the excess minority carrier concentration at t = 0? Well, it was in the dark (and no mention of other outside influences are mentioned) for a long time just before we turned on the light. A “long time” we will soon see, is several lifetimes (). At the point that a “long time” has passed, the system has reached a steady state. For this situation, the semiconductor is at equilibrium just before the light is turned on and Δp = 0 by definition in equilibrium so the initial condition is Δp = 0.
For problems in the spatial domain, the equation will be of second order so two boundary conditions will be needed to find the exact solution. For this step you will need to identify the two boundaries and the values of Dp at those boundaries. The values of Δp at the boundaries will sometimes be stated explicitly and sometimes you will have to deduce it from the situation.
Step 5. Find exact solution
To find the exact solution, plug in the values for the initial/boundary conditions and solve for the unknown term A or terms A and B.
For the example given, we write, 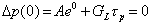 , telling us that A = -GLτp , leading to a final exact solution of,
, telling us that A = -GLτp , leading to a final exact solution of, 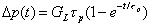 .
.
Step 6. Check answer
The first check one should always make is to compare your answer to the boundary conditions to make sure you did your algebra correctly. We did just fine. One can also imagine what the value for Δp should be and then compare that to the solution. Another check one can make is to compare the result to the low injection to be sure it is a valid solution. Look for the point in space or time that has the highest carrier concentration. Once found compare to the doping concentration and make sure it is much, much less than the doping concentration. In this course we will define much, much less than as being at least 20x smaller. To do this one must have values given for GL and for.
Final thoughts
Any exam problem will have additional questions such as asking for currents, asking whether solutions are valid, integrated recombination, and other evidence that you not only know how to derive solutions, but how to apply them. This will be discussed in the supplement to this lesson.
Look at the continuity equationsThis link was offered under the Continuity Equations lesson, but also has some parts about deriving.