You must login before you can run this tool.
Category
Published on
Abstract
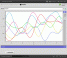
The choice of a function to approximate any given data, is not unique; such function can be found through different methods, in which the parameters of the model are calculated. This tool illustrates the process of sampling from a Gaussian process, to obtain a random function from a process with a given covariance and a mean of zero. Although the results are distributed around zero, this does not imply a loss of generality, since the mean can be changed by adding a function.
The Gaussian process tool takes a set of hyper parameters for a particular covariance function, which is used to calculate a covariance matrix. This matrix is positive definite and Cholesky decomposition can be used to make the sampling process computationally efficient.
References
- Rasmussen, C. E. and C. K. I. Williams (2006). Gaussian processes for machine learning. Cambridge, Mass., MIT Press.
- Langtangen, C.E. (2009). A primer on scientific programming with Python. Springer.
Cite this work
Researchers should cite this work as follows: