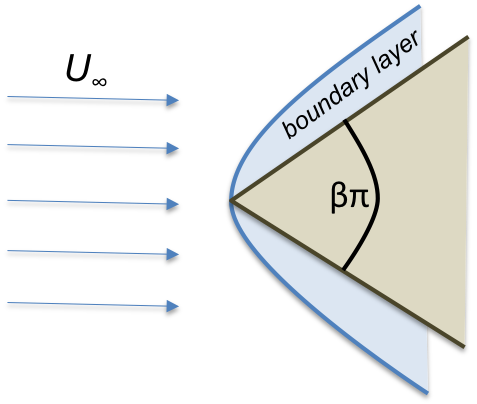
Boundary Layer for Flow Past a Wedge
The Blausius boundary layer velocity solution is a special case of a larger class of problems forflow over a wedge, as shown in the following figure in which $$\beta \pi$$ represents the wedge angle.
The general solution is called the Falkner-Skan boundary layer solution, which starts with a recognition that the free-stream velocity will accelerate for non-zero values of $$\beta$$:
$$u_{e}(x)= U_{0} \left( x/L \right) ^{m}$$
where $$ L $$ is a characteristic length and m is a dimensionless constant that depends on $$\beta$$:
$$ {\beta} = \frac{2m}{m + 1} $$
The condition m = 0 gives zero flow acceleration corresponding to the Blausius solution for flat-plate flow.
We then define a similarity variable $$\eta$$ that combines the local streamwise and cross-flow coordinates x and y (defined relative to the surface of the wedge):
$$ {\eta} = y \sqrt{\frac{U_{0}(m+1)}{2{\nu}L}}\left(\frac{x}{L}\right)^{\frac{m-1}{2}} $$
Then, defining a function f that relates to the streamwise and cross-flow velocities, a single ordinary differential equation ensues from boundary layer momentum and mass conservation:
$$ \frac{\mathrm{d}^3 f}{\mathrm{d} \eta ^3}+f\frac{\mathrm{d}^2 f}{\mathrm{d} \eta^2}+ \beta \left[1-\left(\frac{\mathrm{d}f}{\mathrm{d}\eta}\right)^2 \right]=0 $$
This non-linear equation is not amenable to an exact solution (even for the Blausius solution $$\beta=0$$, which eliminates the last term on the right side). The following Mathematic CDF file solves the equation numerically and provides the streamwise velocity normalized by the local freestream velocity as a function of $$\eta$$.
CDF Tool [1]
^ Numerical Solution of the Falkner-Skan Equation for Various Wedge Angles, from the Wolfram Demonstrations Project //demonstrations.wolfram.com/NumericalSolutionOfTheFalknerSkanEquationForVariousWedgeAngl/